问题描述
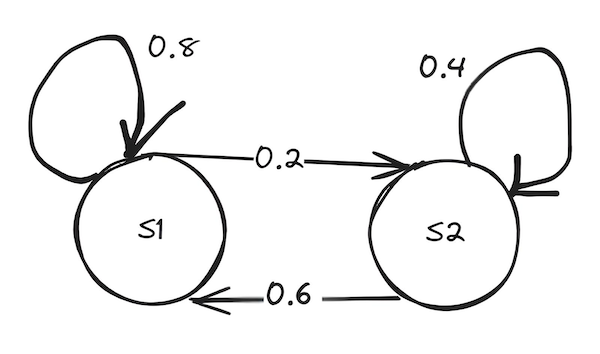
状态沿着马尔可夫链(Markov chain)按照一定概率规则(转移矩阵)转移,下一步往哪转怎么转只和当前状态有关,和之前状态无关。某一条链:
$$S_1 \rightarrow S_2 \rightarrow S_2 \rightarrow S_1 \rightarrow …$$
一段时间后,经过$S_1$和$S_2$的频率(或概率)是多少?和转移依据的规则肯定有关系,那是什么关系?每条连经过两个状态的比例都相同吗?
算一算
状态向量(state vector)为一个概率向量(state vector), 如:
$$\mathbf{w} = \begin{bmatrix} w_1 \\ w_2\end{bmatrix}= \begin{bmatrix} 0.9 \\ 0.1\end{bmatrix}$$
表示此时在状态$S_1$的概率为0.9,在状态$S_2$的概率为0.1。
转移矩阵(transition matrix)是一个随机矩阵(stochastic matrix):
$$P = \begin{bmatrix} p_{11} & p_{21}\\ p_{12} & p_{22} \end{bmatrix}=\begin{bmatrix} 0.8 & 0.6\\ 0.2 & 0.4 \end{bmatrix}$$
$p_{ij}$表示从状态$S_i$到状态$S_j$的转移概率。
从任意一个向量出发,经过多次线性变换(linear transformation),如果转移矩阵是正则的(regular),总会收敛到一个平稳状态向量(steady-state vector):
$$\mathbf{w} \leftarrow P\mathbf{w} = \begin{bmatrix} 0.8 & 0.6\\ 0.2 & 0.4 \end{bmatrix} \begin{bmatrix} 0.9 \\ 0.1 \end{bmatrix}=\begin{bmatrix} 0.78 \\ 0.22 \end{bmatrix} $$
$$\mathbf{w} \leftarrow P\mathbf{w} = \begin{bmatrix} 0.8 & 0.6\\ 0.2 & 0.4 \end{bmatrix} \begin{bmatrix} 0.78 \\ 0.22 \end{bmatrix}=\begin{bmatrix} 0.756 \\ 0.244 \end{bmatrix} $$
$$...$$
$$\mathbf{w} \leftarrow P\mathbf{w} = \begin{bmatrix} 0.8 & 0.6\\ 0.2 & 0.4 \end{bmatrix} \begin{bmatrix} 0.75 \\ 0.25 \end{bmatrix}=\begin{bmatrix} 0.75 \\ 0.25 \end{bmatrix} $$
此时,按照转移矩阵为$P$的马尔可夫链收敛至:
$$ \mathbf{w} = \begin{bmatrix} 0.75 \\ 0.25 \end{bmatrix}$$
直观地说,马尔科夫链收敛至平稳后,进入一个状态的概率质量和从它出去的刚好相等,且对每一个状态来说都是如此。系统稳定地在状态间转移,即:
$$P\mathbf{w}=\mathbf{w}$$
此后一直保持平稳:
$$P^k\mathbf{w} = P^{k-1}\mathbf{w} =...=\mathbf{w} $$
几何意义
从线性代数或几何上理解,空间经过多次线性变换(转移矩阵),最终收敛到一个方向,即的特征向量(eigenvector)的方向。空间上的所有点都会逐渐收敛到这个方向。

附 1
Markov原文用的行向量,两种写法等价:
$$P \mathbf{w} \begin{bmatrix} p_{11} & p_{21}\\ p_{12} & p_{22} \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} $$
$$\mathbf{\pi} T = \begin{bmatrix} w_1 & w_2 \end{bmatrix} \begin{bmatrix} p_{11} & p_{12}\\ p_{21} & p_{22} \end{bmatrix} $$
附 2
由特征多项式(Charasteristic polynomial )可判断$P$是否为正则(regular)。只有当转移矩阵为正则矩阵时,马尔科夫链才能收敛到平稳状态。如
$$P= \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} $$
每次线性变换,空间总是沿着$x=y$轴翻转,并不会收敛到稳定向量上。
附 3
因为从一个状态出去的概率总和为1,且每个状态都如此。可证有一个特征值为1。
$$P \mathbf{w} = \lambda \mathbf{w}$$
$$(P-\lambda I)\mathbf{w} = 0$$
$$det(P-\lambda I) =0$$
每列和需要为1,则$\lambda$必为1。
也可以用特征多项式(Characteristic polynomial )证明。
附 4
传说Markov发明这种链是为了反驳“中心极限定理必须在变量独立时才成立”。变量不独立,条件分布,依然收敛。
附 5
Python code
import numpy as np
# Define the transition matrix
P = np.array([[0.8, 0.6], [0.2, 0.4]])
# Initial state probability distribution
w = np.array([0.9, 0.1])
# To store the state probabilities over iterations
state_probabilities = [w.tolist()]
# Perform several iterations
for _ in range(10):
w = np.dot(P, w)
state_probabilities.append(w.tolist())
state_probabilities
参考资料